三方陣とは3×3の正方形状のマス目(ここでは、行列で表すことにします。)に
1から9までの自然数一つずつを配置し、行、列、対角上の和が全て等しくなっているものです。
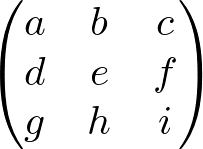
aからiまでは1から9までの自然数が一つずつ入るので、
aからiまでの和 = 1から9までの和 = 45
となります。
条件から
a + b + c = d + e + f = g + h + i = M
なので、
a + b + c + d + e + f + g + h + i = 45
(a + b + c) + (d + e + f) + (g + h + i) = 45
3M = 45
M = 15
となります。
各行、列、対角上の和を書き下すと次のようになります。
a + b + c = 15
d + e + f = 15
g + h + i = 15
a + d + g = 15
b + e + h = 15
c + f + i = 15
a + e + i = 15
c + f + i = 15
a + b + c = 15
d + e + f = 15
g + h + i = 15
a + d + g = 15
b + e + h = 15
c + f + i = 15
a + e + i = 15
c + f + i = 15
ここで、次の条件での15の分割考えます。
・互いに異なる3つの和
・1から9までを用いる
この15の分割を全て挙げると、
15 = 1 + 5 + 9
15 = 1 + 6 + 8
15 = 2 + 4 + 9
15 = 2 + 5 + 8
15 = 2 + 6 + 7
15 = 3 + 4 + 8
15 = 3 + 5 + 7
15 = 4 + 5 + 6
となります。
さて、三方陣の各行、列、対角の和は上の分割になっています。
さらに、各行、列、対角の和は互いに異なり、上の分割の個数と等しいです(3行、3列、2対角の合計8)。
よって、各行、列、対角の和と上の分割は一対一に対応しています。
このことは、分割で使われている整数が三方陣のaからiのどれかであることも示しています。
各行、列、対角の和に登場する各マスの登場回数を数えると、
e: 4回
a, c, g, i: 3回
b, d, f, h: 2回
です。同様に、分割に登場する各整数の個数を数えると、
5: 4回
2, 4, 6, 8: 3回
1, 3, 7, 9: 2回
です。一対一対応から、登場回数も対応します。
従って、
e = 5
が分かります。
次に、a, c, g, i は2, 4, 6, 8のどれかですが、魔方陣の対称性から、
a = 2としても問題ありません。
すると、2 + 5 + i = 15なので、i = 8と決まります。
さらに、魔方陣の対称性から、c = 4としてもOKです。
すると、g = 6と決まります。
最後に、b, d, f, hは各行、列和が15であるので、
b = 9, d = 7, f = 3, h = 1
となります。





