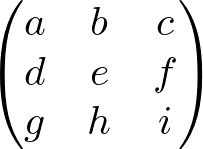ツイッター自作問題 解答4

 このツイートの問題の答えです。

＜問題＞
次の定積分を実行してください。 pic.twitter.com/roFWR1qrYp

— toyo (@toyo9) October 25, 2019

オイラーの公式
$$
e^{ix}=\cos(x)+i\sin(x)
$$
 を用いて、与式を変形すると、

\begin{align*} \int_{-\pi}^{\pi}\sin(x)^{2n}dx &= \int_{-\pi}^{\pi}(\frac{e^{ix}-e^{-ix}}{2i})^{2n}dx \\ &= \frac{1}{(2i)^{2n}}\int_{-\pi}^{\pi}(e^{ix}-e^{-ix})^{2n}dx \\ &= \frac{(-1)^n}{2^{2n}}\int_{-\pi}^{\pi}(e^{i\pi}-e^{-i\pi})^{2n}dx, \end{align*}

ここで、$u=e^{ix}$とおくと、$du=ie^{ix}dx, dx=du/(iu)$で、積分範囲は$|u|=1$を反時計回りに回る範囲となります。従って、

\begin{align*} \frac{(-1)^n}{2^{2n}}&\int_{-\pi}^{\pi}(e^{i\pi}-e^{-i\pi})^{2n}dx \\ &= \frac{(-1)^n}{2^{2n}}\oint_{|u|=1を反時計回り}(u-u^{-1})^{2n}\frac{du}{iu}\\ &=\frac{(-1)^n}{2^{2n}i}\oint_{|u|=1を反時計回り} (\dots+(-1)^n \binom{2n}{n}+\cdots)\frac{du}{u} \\ &=\frac{(-1)^n}{2^{2n}i}\oint_{|u|=1を反時計回り} (\dots+(-1)^n \binom{2n}{n}\frac{1}{u}+\cdots)du,  \\ \end{align*}

留数計算より、

\begin{align*} \frac{(-1)^n}{2^{2n}i}&\oint_{|u|=1を反時計回り} (\dots+(-1)^n \binom{2n}{n}\frac{1}{u}+\cdots)du \\ &= \frac{(-1)^n}{2^{2n}i}(-1)^n \binom{2n}{n}2\pi i \\ &= \frac{\pi}{2^{2n-1}} \binom{2n}{n}, \end{align*}

よって最終的に、
$$
\int_{-\pi}^{\pi}\sin(x)^{2n}dx = \frac{\pi}{2^{2n-1}} \binom{2n}{n}
$$
となります。

ツイッター自作問題 解答3

このツイートの問題の解答です。

＜問題＞
次の不等式を証明してください。
Σ_{p:prime}は、pを素数全体に動かして和を取ります。 pic.twitter.com/gaNHZ2syqC

— toyo (@toyo9) September 10, 2019

まず、上界を評価します。この評価には、リーマンゼータ関数$\zeta (s)$を用います。リーマンゼータ関数は、次のように定義されています。
$$
\zeta (s) := \sum_{k=1}^{\infty} \frac{1}{k^s}\;\;\;
(s \in \mathbb{C}, {\rm Re}(s) > 1)
$$
特に、次のオイラー積と呼ばれるリーマンゼータ関数の無限積表示を用います。

定理(リーマンゼータ関数のオイラー積)
$$
\zeta (s) = \prod_{p:{\rm prime}}\frac{1}{1-\frac{1}{p^s}}
$$
ここで、$\prod_{p:{\rm prime}}$は、$p$を素数全体に動かして積を取ることを表します。
証明:

\begin{align*} \zeta(s) &= 1 + \frac{1}{2^s} + \frac{1}{3^s} + \frac{1}{4^s} + \frac{1}{5^s}+ \frac{1}{6^s} + \cdots \\ &= \frac{1}{2^s}\left(1 + \frac{1}{2^s} + \frac{1}{3^s} + \cdots \right) + 1 + \frac{1}{3^s} + \frac{1}{5^s} + \cdots \\ &= \frac{1}{2^s}\zeta(s) + 1 + \frac{1}{3^s} + \frac{1}{5^s} + \cdots \\ \left(1 - \frac{1}{2^s}\right)&\zeta(s) = 1 + \frac{1}{3^s} + \frac{1}{5^s} + \cdots \\ &= \frac{1}{3^s}\left(1 + \frac{1}{3^s} + \cdots \right) + 1 + \frac{1}{5^s} + \cdots \\ &= \frac{1}{3^s}\left(1 - \frac{1}{2^s}\right)\zeta(s) + 1 + \frac{1}{5^s} + \cdots \\ \left(1 - \frac{1}{2^s}\right)&\left(1 - \frac{1}{3^s}\right)\zeta(s) = 1 + \frac{1}{5^s} + \cdots &\cdots \end{align*}

同様の変形を繰り返すと、
\begin{align*}
\prod_{p:{\rm prime}}\left(1-\frac{1}{p^s} \right) \zeta (s) &= 1 \\
\zeta (s) &= \prod_{p:{\rm prime}}\frac{1}{1-\frac{1}{p^s}}
\end{align*}
となり、結果が示されました。$\square$

さて、良く知られた結果である$\zeta (2) = \pi^2/6$をオイラー積で表すと、
$$
\prod_{p:{\rm prime}}\frac{1}{1-\frac{1}{p^2}} = \frac{\pi^2}{6}
$$
となります。両辺を入れ替えてから、両辺の対数を取って変形して行くと、

\begin{align*} \log \left(\frac{\pi^2}{6}\right) &= \log \left(\prod_{p:{\rm prime}}\frac{1}{1-\frac{1}{p^2}}\right) \\ &= \sum_{p:{\rm prime}}\log \left(\frac{1}{1-\frac{1}{p^2}}\right) \\ &= \sum_{p:{\rm prime}}\left(\frac{1}{p^2}+\frac{1}{2p^4}+\frac{1}{3p^6} + \cdots \right)\\ &= \sum_{p:{\rm prime}}\frac{1}{p^2} + \sum_{p:{\rm prime}}\left(\frac{1}{2p^4} + \frac{1}{3p^6} + \cdots \right) \\ &> \sum_{p:{\rm prime}}\frac{1}{p^2} + \frac{1}{2\times 2^4} + \frac{1}{3\times 2^6} + \cdots \\ &= \sum_{p:{\rm prime}}\frac{1}{p^2} - \log \left(1-\frac{1}{4} \right) - \frac{1}{4} \\ \log \left(\frac{\pi^2}{6}\right) &+ \log \left(\frac{3}{4} \right) + \frac{1}{4} > \sum_{p:{\rm prime}}\frac{1}{p^2} \\ &\log \left(\frac{\pi^2}{8}\right) + \frac{1}{4} > \sum_{p:{\rm prime}}\frac{1}{p^2} \end{align*}

となり、上界を求められました。

一方、下界ですが、最初の3項だけ足して求めた下界、つまり、
$$
\sum_{p:{\rm prime}}\frac{1}{p^2} > \frac{1}{2^2} + \frac{1}{3^2} + \frac{1}{5^2} = \frac{361}{900} = 0.40\dot{1}
$$
の方が問題にある下界$(\log(\pi^2/6)-4/3+\pi^2/8=0.398\dots$)より、良い評価となっています。

ツイッター自作問題 解答1,2

この2つのツイートの問題の答えです。

https://t.co/phciCAXk84

— toyo (@toyo9) April 20, 2019

https://t.co/fQ2odlBgV9

— toyo (@toyo9) April 20, 2019

無理数の$2/3$乗は、必ずしも無理数にはなりません。
例：
$$
x := 2^{\frac{3}{2}}
$$
とすると、$x$は無理数ですが、
$$
x^{\frac{2}{3}}=2^{\frac{3}{2}\times \frac{2}{3}}
=2^1
=2
$$
となり、$x^{2/3}$は無理数ではありません。

一方で、無理数の平方根($1/2$乗)は、必ず無理数となります。
$x$を正の無理数とし、もし、$x^{1/2}$が有理数だとすると、有理数は積で閉じているので、
$$
x^{\frac{1}{2}}x^{\frac{1}{2}}=x
$$
も有理数となり、矛盾します。
背理法より、$x^{1/2}$が有理数でない、つまり無理数であることが分かります。

線形代数 n次元ベクトル、行列とそれらの演算

線形代数の主役である、n次元ベクトルと行列について述べます。n次元ベクトルとは、数(実数など体の元)をn個縦か横に並べたものです。縦に並べたものを縦ベクトルまたは列ベクトル、横に並べたものを横ベクトルまたは行ベクトルと呼びます。
例：
$$
2次元縦ベクトル
\begin{pmatrix}
1 \\
2
\end{pmatrix},\;\;
3次元縦ベクトル
\begin{pmatrix}
\pi \\
e \\
\gamma
\end{pmatrix}
$$
$$
2次元横ベクトル
\begin{pmatrix}
73 & 91
\end{pmatrix},\;\;
3次元横ベクトル
\begin{pmatrix}
e+\tau & \sigma & \sqrt{101}
\end{pmatrix}
$$
ここからは特に断らない限りベクトルと言えば、3次元縦ベクトルのこととします。次に、ベクトルの演算についてです。ベクトルに次の3つの演算を定義します。
スカラー(数)$a$, ベクトル${}^t\!\begin{pmatrix}x & y & z \end{pmatrix}$に対して、
$$
\begin{equation}
a\begin{pmatrix}x \\ y \\ z \end{pmatrix}:=
\begin{pmatrix}ax \\ ay \\ az \end{pmatrix}
\end{equation}\;\;(スカラー倍)
$$
2つのベクトル${}^t\!\begin{pmatrix}x_1 & y_1 & z_1 \end{pmatrix}$、${}^t\!\begin{pmatrix}x_2 & y_2 & z_2 \end{pmatrix}$に対して、
$$
\begin{equation}
\begin{pmatrix}x_1 \\ y_1 \\ z_1 \end{pmatrix}
+
\begin{pmatrix}x_2 \\ y_2 \\ z_2 \end{pmatrix}:=
\begin{pmatrix}x_1 + x_2 \\ y_1 + y_2 \\ z_1 + z_2 \end{pmatrix}
\end{equation}\;\;(和)
$$
ただし、和は同じ形状の2つのベクトルにのみ定義されます。
横ベクトル$\begin{pmatrix}x_1 & y_1 & z_1 \end{pmatrix}$、縦ベクトル${}^t\!\begin{pmatrix}x_2 & y_2 & z_2 \end{pmatrix}$に対して、
$$
\begin{equation}
\begin{pmatrix}x_1 & y_1 & z_1 \end{pmatrix}
\begin{pmatrix}x_2 \\ y_2 \\ z_2 \end{pmatrix}:=
x_1 x_2 + y_1 y_2 + z_1 z_2
\end{equation}\;\;(内積)
$$
左側が横ベクトルで右側が縦ベクトルで無ければならず、かつ長さも同じであるベクトルに対して定義されます。
※n次元の複素ベクトルの内積とは異なります。複素ベクトル内積は$\overline{x_1} x_2 + \overline{y_1} y_2 + \overline{z_1} z_2$となります。
例：
$$
\begin{equation*}
3\begin{pmatrix}8 \\ 3 \\ \frac{2}{3} \end{pmatrix}=
\begin{pmatrix}24 \\ 9 \\ 2 \end{pmatrix}
\end{equation*}
$$
$$
\begin{equation*}
\begin{pmatrix}\pi \\ \frac{1}{3} \end{pmatrix}
+
\begin{pmatrix}e - \pi \\ \frac{2}{3} \end{pmatrix}=
\begin{pmatrix}e \\ 1\end{pmatrix}
\end{equation*}
$$
$$
\begin{equation*}
\begin{pmatrix}\sqrt{2} & 2^3 & 0 \end{pmatrix}
\begin{pmatrix}\sqrt{8} \\ 2^4 \\ 1 \end{pmatrix}=
4 + 2^7 + 0 = 132
\end{equation*}
$$

さて、ベクトルについては一段落とし、行列の話に移ります(ベクトルも出てきますが)。n行m列の行列(簡単に(n, m)行列とも呼ぶことにします)とは、mn個の数(実数など体の元)を縦n横mの長方形上に並べたものです。特に、$m=n$の場合は、n次正方行列と呼びます。実は、n行1列の行列はn次元縦ベクトル、1行m列の行列はm次元横ベクトルになっているので、行列はベクトルを一般化したものと見ることもできます。
例：
$$
2行3列の行列
\begin{pmatrix}
 1  &  4 &    7 \\
10 & 13 & 16
\end{pmatrix},\;\;
$$
$$
2行2列の行列(2次正方行列)
\begin{pmatrix}
\pi & e^{\pi} \\
\log(2) & \gamma
\end{pmatrix},\;\;
$$
$$
3行1列の行列(3次元縦ベクトル)
\begin{pmatrix}
e+\tau \\ \sigma \\ \sqrt{101}
\end{pmatrix}
$$
ここから、一般の$(n,m)$行列$\begin{pmatrix}
a_{11} & \dots & a_{1m} \\
\vdots & \ddots & \vdots \\
a_{n1} & \dots & a_{nm}
\end{pmatrix}$を$(a_{ij})$$(1\leqq i \leqq n, 1 \leqq j \leqq m)$と表すことにします。次に、行列の演算についてです。行列に次の3つの演算を定義します。
スカラー(数)$b$, $(n,m)$行列$(a_{ij})$に対して、
$$
\begin{equation}
b(a_{ij}):= (ba_{ij})\;\;(スカラー倍)
\end{equation}
$$

2つの同じ形状の行列$(a_{ij})、(b_{ij})$に対して、
$$
\begin{equation}
(a_{ij})+(b_{ij}):= (a_{ij} + b_{ij})\;\;(和)
\end{equation}
$$
$(n,m)$行列$(a_{ij})$、$(m,l)$行列$(b_{jk})$に対して、
$$
\begin{equation}
(a_{ij})(b_{jk}):=
\left(\sum_{j=1}^{m}a_{ij}b_{jk}\right)
\end{equation}\;\;(積)
$$
例：
$$
2\begin{pmatrix}
 1  &  4 &    7 \\
10 & 13 & 16
\end{pmatrix}
=
\begin{pmatrix}
 2  &  8 &    14 \\
20 & 26 & 32
\end{pmatrix}
$$
$$
\begin{pmatrix}
1 & 3 \\
9 & 0
\end{pmatrix}
+
\begin{pmatrix}
-4 & 7 \\
12 & 5
\end{pmatrix}
=
\begin{pmatrix}
-3 & 10 \\
21 & 5
\end{pmatrix}
$$
\begin{align*}
\begin{pmatrix}
 1  &  4 &    7 \\
10 & 13 & 16
\end{pmatrix}
\begin{pmatrix}
 4  &  2 \\
1 & 3 \\
5 & 6
\end{pmatrix}
=
\begin{pmatrix}
43  &  56 \\
133 & 155
\end{pmatrix}\\
\end{align*}
\begin{align*}
メモ:
43 &= 1\times 4+4\times 1 + 7\times 5 \\
56 &= 1\times 2+4\times 3 + 7\times 6 \\
133 &= 10\times 4+13\times 1 + 16\times 5 \\
155 &= 10\times 2+13\times 3 + 16\times 6
\end{align*}
行列を扱う重要な方法として、ベクトルを並べたものとして扱う手があります。
例：
$$
A
=
\begin{pmatrix}
1  &  7 \\
8 & 15
\end{pmatrix}
=
\begin{pmatrix}
v_1  &  v_2
\end{pmatrix}
=
\begin{pmatrix}
{}^t\!w_1  \\
{}^t\!w_2
\end{pmatrix}
$$
$$
v_1
=
\begin{pmatrix}
1\\
8
\end{pmatrix}
,\;\;
v_2
=
\begin{pmatrix}
7\\
15
\end{pmatrix}
,\;\;
w_1
=
\begin{pmatrix}
1\\
7
\end{pmatrix}
,\;\;
w_2
=
\begin{pmatrix}
8\\
15
\end{pmatrix}
$$
そして、2つの行列$A=\begin{pmatrix}{}^t\!w_1  \\{}^t\!w_2
\end{pmatrix}$、$B=\begin{pmatrix}v_1  &  v_2 \end{pmatrix}$に対して、$AB$は次のように計算することができます。
$$
AB
=
\begin{pmatrix}Av_1  &  Av_2 \end{pmatrix}
=
\begin{pmatrix}{}^t\!w_{1}B  \\{}^t\!w_{2}B\end{pmatrix}
=
\begin{pmatrix}
{}^t\!w_1 v_1  &  {}^t\!w_1 v_2 \\
{}^t\!w_2 v_1 & {}^t\!w_2 v_2
\end{pmatrix}
$$
行列の積は複雑ですが、行列をベクトルを並べたものとして考え、ベクトルの内積を用いると見やすくなるのではと思います。

線形代数 固有値問題 具体例1

次の行列$A$の固有値、固有ベクトルを求め、$A$を対角化します。
$$
A =
\begin{pmatrix}
2 & 1 \\
1 & 2
\end{pmatrix}
$$
$A$の固有値を$\lambda$、固有ベクトルを$v$とすると、
$$
\begin{align*}
Av  &= \lambda v \\
(A - \lambda E)v &= 0
\end{align*}
$$
$v\neq 0$とすると、$(A - \lambda E)$は正則でないので、
$$
\begin{align*}
|A - \lambda E| &= 0 \\
\begin{vmatrix}
2- \lambda & 1 \\
1 & 2 - \lambda
\end{vmatrix} &= 0 \\
(2- \lambda)^2 - 1 &= 0 \\
(1- \lambda)(3- \lambda) &= 0
\end{align*}
$$
よって、
$$
\lambda = 1 または 3
$$
となります。$\lambda_1 = 1、\lambda_2 = 3$とし、$\lambda_1$対する固有ベクトルを$v_1={}^t\!\begin{pmatrix}x_1 & y_1\end{pmatrix}$、$\lambda_2$対する固有ベクトルを$v_2={}^t\!\begin{pmatrix}x_2 & y_2\end{pmatrix}$とします。$v_1$を求めることにすると、
\begin{align*}
(A - \lambda_1 E)v_1 &= 0 \\
\begin{pmatrix}
1 & 1 \\
1 & 1
\end{pmatrix}
\begin{pmatrix}
x_1 \\
y_1
\end{pmatrix}
&=
\begin{pmatrix}
0 \\
0
\end{pmatrix}
\end{align*}
これを満たす$v_1$として、
$$
v_1
=
\begin{pmatrix}
1 \\
-1
\end{pmatrix}
$$
を取ります。次に、$v_2$を求めることにすると、
\begin{align*}
(A - \lambda_2 E)v_2 &= 0 \\
\begin{pmatrix}
-1 & 1 \\
1 & -1
\end{pmatrix}
\begin{pmatrix}
x_2 \\
y_2
\end{pmatrix}
&=
\begin{pmatrix}
0 \\
0
\end{pmatrix}
\end{align*}
これを満たす$v_2$として、
$$
v_2
=
\begin{pmatrix}
1 \\
1
\end{pmatrix}
$$
を取ります。よって、$A$の2つ持つ固有値と固有ベクトルの組として、
$$
(1, \begin{pmatrix}1 \\ -1\end{pmatrix}), (3, \begin{pmatrix}1 \\ 1\end{pmatrix})
$$
が取れます。$P=\begin{pmatrix}v_1 & v_2 \end{pmatrix}$とおいて、Aを対角化すると、
\begin{align*}
AP &= A\begin{pmatrix}v_1 & v_2 \end{pmatrix} \\
     &= \begin{pmatrix}Av_1 & Av_2 \end{pmatrix} \\
     &= \begin{pmatrix}1v_1 & 3v_2 \end{pmatrix} \\
     &= \begin{pmatrix}v_1 & v_2 \end{pmatrix}
           \begin{pmatrix}1 & 0 \\
                                   0 & 3
           \end{pmatrix} \\
     &= P
           \begin{pmatrix}1 & 0 \\
                                   0 & 3
           \end{pmatrix} \\
A &= P
           \begin{pmatrix}1 & 0 \\
                                   0 & 3
           \end{pmatrix}
        P^{-1} \\
\begin{pmatrix}
2 & 1 \\
1 & 2
\end{pmatrix}
&=
\begin{pmatrix}
1 & 1 \\
-1 & 1
\end{pmatrix}
\begin{pmatrix}
1 & 0 \\
0 & 3
\end{pmatrix}
\begin{pmatrix}
1 & 1 \\
-1 & 1
\end{pmatrix}^{-1}
\end{align*}
となります。

数学でよく使われる記号

$\mathbb{N}$:自然数の集合

$\mathbb{Z}$:整数の集合

$\mathbb{Q}$:有理数の集合

$\mathbb{R}$:実数の集合

$\mathbb{C}$:複素数の集合

集合$S$に対して、
$a\in S$:aはSの元(要素)である。

集合$A, B$に対して、全てのAの元がBの元でもあるとき、
$A \subset B$:$A$は$B$の部分集合である。

行列$A$に対して、${}^t\!A$は$A$の転置行列を表す。
$$
{}^t\!
\begin{pmatrix}
1 & 2 & 3 \\
4 & 5 & 6
\end{pmatrix}
=
\begin{pmatrix}
1 & 4  \\
2 & 5  \\
3 & 6
\end{pmatrix}
$$
$$
{}^t\!
\begin{pmatrix}
1 \\
2 \\
3
\end{pmatrix}
=
\begin{pmatrix}
1 & 2 & 3 \\
\end{pmatrix}
$$

線形代数 対角化と固有値問題

メモ:徐々に色々書き足す予定
正方行列の対角化についてです。
対角化とは、$n$次正方行列$A$を次のように表すことを言います。
\begin{align*}
A = PDP^{-1}
\end{align*}
ここで$P$は正則行列($P^{-1}$はその逆行列)、$D$は対角行列で、
$$
D =
\begin{pmatrix}
\lambda_{1} & &\\
 & \ddots & \\
 & & \lambda_{n}
\end{pmatrix}
$$
です。
例
\begin{align*}
&\begin{pmatrix}
5 &4 \\
-8 &-7
\end{pmatrix}
=
\begin{pmatrix}
1 &-1 \\
-1 &2
\end{pmatrix}
\begin{pmatrix}
1 &0\\
0 &-3
\end{pmatrix}
\begin{pmatrix}
1 &-1 \\
-1 &2
\end{pmatrix}^{-1}
\\
&\begin{pmatrix}
2 &3 &3\\
3 &2 &3 \\
3 &3 &2
\end{pmatrix}
=
\\
&\begin{pmatrix}
1 &1 &1\\
-1 &0 &1 \\
0 &-1 &1
\end{pmatrix}
\begin{pmatrix}
-1 &0 &0\\
0 &-1 &0 \\
0 &0 &8
\end{pmatrix}
\begin{pmatrix}
1 &1 &1\\
-1 &0 &1 \\
0 &-1 &1
\end{pmatrix}^{-1}
\end{align*}
どのような$A$でも、対角化できるわけではありません(条件などについては、今のところ触れないでおくことにします)。
対角化には、次の利点があります。
・$A^m(m\in\mathbb{N})$が簡単に求められる。
例
\begin{align*}
A^{4}
&= (PDP^{-1})(PDP^{-1})(PDP^{-1})(PDP^{-1}) \\
&= PD(P^{-1}P)D(P^{-1}P)D(P^{-1}P)DP^{-1} \\
&= PDDDDP^{-1} \\
&= PD^{4}P^{-1}
\end{align*}
そして、
\begin{align*}
D^4 &=
\begin{pmatrix}
\lambda_{1} & &\\
 & \ddots & \\
 & & \lambda_{n}
\end{pmatrix}^{4}\\
&=
\begin{pmatrix}
\lambda_{1}^{4} & &\\
 & \ddots & \\
 & & \lambda_{n}^{4}
\end{pmatrix}
\end{align*}
となり、簡単に計算できます。
メモ:ここはもっと増やしたい。よく使う記号を他の記事でまとめる。

さて、ここからは$A$を3行3列の行列とし、$P$を縦ベクトルを三本($v_1, v_2, v_3$)並べたものと見て、
$$
P=
\begin{pmatrix}
v_1 &v_2 &v_3
\end{pmatrix}
$$
$$
v_1 =
\begin{pmatrix}
x_1 \\
y_1 \\
z_1
\end{pmatrix}, \;\;\;
v_2 =
\begin{pmatrix}
x_2 \\
y_2 \\
z_2
\end{pmatrix}, \;\;\;
v_3 =
\begin{pmatrix}
x_3 \\
y_3 \\
z_3
\end{pmatrix}
$$
とします。すると、
\begin{align*}
A &= PDP^{-1} \\
AP &= PD \\
A\begin{pmatrix}v_1 &v_2 &v_3\end{pmatrix} &=
\begin{pmatrix}
x_1 &x_2 & x_3 \\
y_1 &y_2 & y_3 \\
z_1 &z_2 & z_3
\end{pmatrix}
\begin{pmatrix}
\lambda_{1} & &\\
 & \lambda_{2} & \\
 & & \lambda_{3}
\end{pmatrix} \\
\begin{pmatrix}Av_1 &Av_2 &Av_3\end{pmatrix} &=
\begin{pmatrix}
\lambda_{1}x_1 &\lambda_{2}x_2 & \lambda_{3}x_3 \\
\lambda_{1}y_1 &\lambda_{2}y_2 & \lambda_{3}y_3 \\
\lambda_{1}z_1 &\lambda_{2}z_2 & \lambda_{3}z_3
\end{pmatrix} \\
\begin{pmatrix}Av_1 &Av_2 &Av_3\end{pmatrix}
&=
\begin{pmatrix}
\lambda_{1}v_1&
\lambda_{2}v_2&
\lambda_{3}v_3
\end{pmatrix}
\end{align*}
より、
\begin{align*}
Av_i=\lambda_{i}v_i\;\;\;(i = 1,2,3)
\end{align*}
を満たします。一般に、正方行列$A$に対して、
\begin{align}
Av=\lambda v
\end{align}
を満たす組$(\lambda, v)$を求める問題を固有値問題と呼びます。
$\lambda$を固有値、$v$を固有ベクトルと呼びます。
つまり、$A$の固有値と固有ベクトルを求めることができれば、(基本的に)$A$を対角化することができます。

固有値問題の解き方について見ていきます。
$(1)$を変形すると、
\begin{align*}
Av - \lambda v &= 0 \;\;\;(0:零ベクトル)\\
Av - \lambda E v&=0\;\;\;(E:単位行列)\\
(A - \lambda E)v &= 0
\end{align*}
と表せます。もし、$A - \lambda E$の逆行列が存在すると、$v=0$となる自明な解しか求められません。なので、$(A - \lambda E)^{-1}$は存在しないとします。すると、$(A - \lambda E)^{-1}$が存在しないならば、$|A - \lambda E|=0$を満たします。
つまり、
\begin{align*}
|A - \lambda E|=0
\end{align*}
を解くことにより、固有値$\lambda$を求めることができます。
後は、各固有値$\lambda$に対して、$(1)$を解くことで対応する固有ベクトルを求めることができます。
計算例1

三方陣 分割を用いた解法

魔方陣の一種である三方陣を「整数の分割」(もしくは「分割」)を用いて求めます。

三方陣とは3×3の正方形状のマス目(ここでは、行列で表すことにします。)に

1から9までの自然数一つずつを配置し、行、列、対角上の和が全て等しくなっているものです。

まず、各行、列、対角上の和(=Mとします。)を求めます。

aからiまでは1から9までの自然数が一つずつ入るので、

aからiまでの和 = 1から9までの和 = 45

となります。

条件から

a + b + c = d + e + f = g + h + i = M

なので、

a + b + c + d + e + f + g + h + i = 45

(a + b + c) + (d + e + f) + (g + h + i) = 45

3M = 45

M = 15

となります。

各行、列、対角上の和を書き下すと次のようになります。

a + b + c = 15
d + e + f = 15
g + h + i = 15
a + d + g = 15
b + e + h = 15
c + f + i = 15
a + e + i = 15
c + f + i = 15

一方で、分割とは正整数を正整数の和で表す方法のことです。

ここで、次の条件での15の分割考えます。
・互いに異なる3つの和
・1から9までを用いる
この15の分割を全て挙げると、

15 = 1 + 5 + 9
15 = 1 + 6 + 8
15 = 2 + 4 + 9
15 = 2 + 5 + 8
15 = 2 + 6 + 7
15 = 3 + 4 + 8
15 = 3 + 5 + 7
15 = 4 + 5 + 6

となります。
さて、三方陣の各行、列、対角の和は上の分割になっています。
さらに、各行、列、対角の和は互いに異なり、上の分割の個数と等しいです(3行、3列、2対角の合計8)。
よって、各行、列、対角の和と上の分割は一対一に対応しています。

このことは、分割で使われている整数が三方陣のaからiのどれかであることも示しています。
各行、列、対角の和に登場する各マスの登場回数を数えると、
e: 4回
a, c, g, i: 3回
b, d, f, h: 2回
です。同様に、分割に登場する各整数の個数を数えると、
5: 4回
2, 4, 6, 8: 3回
1, 3, 7, 9: 2回
です。一対一対応から、登場回数も対応します。
従って、
e = 5
が分かります。

次に、a, c, g, i は2, 4, 6, 8のどれかですが、魔方陣の対称性から、
a = 2としても問題ありません。
すると、2 + 5 + i = 15なので、i = 8と決まります。

さらに、魔方陣の対称性から、c = 4としてもOKです。
すると、g = 6と決まります。

最後に、b, d, f, hは各行、列和が15であるので、
b = 9, d = 7, f = 3, h = 1
となります。

これで、三方陣を求めることができました。

算数クイズ 回答

このツイートの問題の回答です。

【算数クイズ】
面白い問題ができた！
１から９までの数を１回ずつ使う、分数の問題です。

答えるときはリプライは避け、引用RTなどでお願いします！✨
RTで多くの人に届けてください～～！！ pic.twitter.com/NQgwZP1X1i

— 横山 明日希 -新メンバー募集中- (@asunokibou) 2019年1月26日

等式、

を考えます。

この等式が問題の条件を満たすとします。つまり、

ア = am ・・・(1)

イ = an  ・・・(2)

ウ = bm ・・・(3)

エ + オ = bn ・・・(4)

カ = cm ・・・(5)

キ + ク + ケ = cn ・・・(6)

を満たします。エ < オ, キ < ク < ケ とします(一般性を保ちます)。

すると、1から9までの自然数の和は45であるから、

が成り立ちます。

これから、

を満たします(a|b: aがbを割り切る)。

よって、

のa+b+cとm+nの組み合わせの候補が取れます。

a

となります。

ここからは、この2パターンを場合分けして、調べます。

＜a + b + c = 9, m + n = 5の場合＞

以下のa, b, cの組み合わせの候補が取れます。

この全ての組み合わせにおいて、m = 1, n = 4となります((5):カ = cm ≦ 9 と am ≠ bmから導かれます)。

(a, b, c) = (1, 2, 6)の場合

(1)から(6)を書き直すと、

ア = am = 1

イ = an = 4

ウ = bm = 2

エ + オ = bn = 8

カ = cm = 6

キ + ク + ケ = cn = 24

問題の条件(アからケは1から9の一つずつ当てはまる)から

エ = 3, オ = 5, キ = 7, ク = 8, ケ = 9

と決定できます。

よって、

が見つけられます。

(a, b, c) = (1, 3, 5)の場合

(1)から(6)を書き直すと、

ア = am = 1

イ = an = 4

ウ = bm = 3

エ + オ = bn = 12

カ = cm = 5

キ + ク + ケ = cn = 20

この場合は、解がありません(例えば、エとオに当てはまる数が取れない)。

(a, b, c) = (2, 3, 4)の場合

(1)から(6)を書き直すと、

ア = am = 2

イ = an = 8

ウ = bm = 3

エ + オ = bn = 12

カ = cm = 4

キ + ク + ケ = cn = 16

問題の条件から

エ = 5, オ = 7, キ = 1, ク = 6, ケ = 9

と決定できます。

よって、

が見つけられます。

＜a + b + c = 15, m + n = 3の場合＞

以下のa, b, cの組み合わせの候補が取れます。

この全ての組み合わせにおいて、m = 1, n = 2となります((5):カ = cm ≦ 9から導かれます)。

(a, b, c) = (1, 5, 9)の場合

(1)から(6)を書き直すと、

ア = am = 1

イ = an = 2

ウ = bm = 5

エ + オ = bn = 10

カ = cm = 9

キ + ク + ケ = cn = 18

問題の条件から、

エ = 3, オ = 7, キ = 4, ク = 6, ケ = 8
と
エ = 4, オ = 6, キ = 3, ク = 7, ケ = 8

が取れます。

よって、

が見つけられます。

(a, b, c) = (1, 6, 8)の場合

(1)から(6)を書き直すと、

ア = am = 1

イ = an = 2

ウ = bm = 6

エ + オ = bn = 12

カ = cm = 8

キ + ク + ケ = cn = 16

問題の条件から、

エ = 3, オ = 9, キ = 4, ク = 5, ケ = 7
と
エ = 5, オ = 7, キ = 3, ク = 4, ケ = 9

が取れます。

よって、

が見つけられます。

(a, b, c) = (2, 4, 9)の場合

(1)から(6)を書き直すと、

ア = am = 2

イ = an = 4

ウ = bm = 4
エ + オ = bn = 8

カ = cm = 9

キ + ク + ケ = cn = 18

この場合は、解がありません。

(a, b, c) = (2, 5, 8)の場合

(1)から(6)を書き直すと、

ア = am = 2

イ = an = 4

ウ = bm = 5

エ + オ = bn = 10

カ = cm = 8

キ + ク + ケ = cn = 16

問題の条件から、

エ = 1, オ = 9, キ = 3, ク = 6, ケ = 7
と
エ = 3, オ = 7, キ = 1, ク = 8, ケ = 9

が取れます。

よって、

が見つけられます。

(a, b, c) = (2, 6, 7)の場合

(1)から(6)を書き直すと、

ア = am = 2

イ = an = 4

ウ = bm = 6

エ + オ = bn = 12

カ = cm = 7

キ + ク + ケ = cn = 14

問題の条件から、

エ = 3, オ = 9, キ = 1, ク = 5, ケ = 8
が取れます。
よって、

が見つけられます。

(a, b, c) = (3, 4, 8)の場合

(1)から(6)を書き直すと、

ア = am = 3

イ = an = 6

ウ = bm = 4

エ + オ = bn = 8

カ = cm = 8

キ + ク + ケ = cn = 16

問題の条件から、

エ = 1, オ = 7, キ = 2, ク = 5, ケ = 9
が取れます。
よって、

が見つけられます。

(a, b, c) = (3, 5, 7)の場合

(1)から(6)を書き直すと、

ア = am = 3

イ = an = 6

ウ = bm = 5

エ + オ = bn = 10

カ = cm = 7

キ + ク + ケ = cn = 14

問題の条件から、

エ = 1, オ = 9, キ = 2, ク = 4, ケ = 8
と
エ = 2, オ = 8, キ = 1, ク = 4, ケ = 9
が取れます。
よって、

が見つけられます。

(a, b, c) = (4, 5, 6)の場合

(1)から(6)を書き直すと、

ア = am = 4

イ = an = 8

ウ = bm = 5

エ + オ = bn = 10

カ = cm = 6

キ + ク + ケ = cn = 12

問題の条件から、

エ = 1, オ = 9, キ = 2, ク = 3, ケ = 7
と
エ = 3, オ = 7, キ = 1, ク = 2, ケ = 9
が取れます。
よって、

が見つけられます。